Note from author: In this article as pressure units I use BAR. If you prefer or operate on PSI units remember that pressure of 1 BAR is about 14,5 PSI.
An integral piece of equipment for any diver – recreational or technical – is a diving cylinder. It is used in every possible equipment configuration regardless of whether it is open (OC) or closed circuit (CC). This important piece of diving equipment provides us with the necessary supply of breathing gas to stay underwater for a certain amount of time. Of course, we would like this time to be as long as possible. Manufacturers, responding to the needs of divers, supplied the market with cylinders of increasingly larger volumes. Divers, in turn, combined them into sets known to all as “twinsets”. However, a large cylinder (or cylinders) on the diver’s back is not only longer time underwater. It’s also a heavier weight to carry, larger size, problems with transport to the dive site or harder set to moving whit it underwater. So unless a diver is able to spend a lot of money on closed-circuit diving equipment, he or she is doomed to a severely limited time under water. A time that in turn – with our diving progress – gets shorter and shorter as we dive deeper or farther.
Advantages of 300-bar cylinders.
However, for OC users there is another option they can use. Divers can also use cylinders that are adapted for operation at 300 bar instead of the standard 200 bar. Such solution has several important advantages. First of all, higher pressure means a larger gas reserve without the need to increase the cylinder’s volume. This fact makes such solution very beneficial for people of smaller posture who do not want to carry large and bulky sets on their backs. Moreover, large cylinders sometimes make harder moving in confined spaces (e.g. inside a wreck) so smaller set sounds reasonable. Another advantage of 300-bar cylinders is the reduction of additional weight that diver must to take underwater. Because of the need to operate at much higher pressures, 300-bar cylinders must have a thicker walls than their standard counterparts of the same volumes. The difference therefore affects their overall weight. A standard 12-liter diving cylinder weighs about 14 kg, while its more robust sister of the same volume weighs as much as 17 kg. This difference allows us to significantly reduce the ballast attached to the sets, and spreading the weight over a larger area will enable us to trim more easily.
Why 300-bar cylinders are not so popular?

The only disadvantage – besides the price, of course – of such solution is an equipment compatibility. While there are no problems in this field with scuba regulators (practically all 1st stage with DIN-type connection available on the market are adapted to work at pressure 300 bar), finding a compressor that is capable of filling such a tank can be a certain difficulty. Large dive centers and bases mostly have the appropriate equipment. However, it is practically impossible to fill this type of cylinders to such high pressure using portable compressors or in less popular diving places.
(Image: “300 BAR” mark on scuba regulator’s 1st stage with DIN-type connection.)
Is “300 bar” means more?
Nevertheless, hundreds of divers around the world use this type of cylinders. Many of them as the main reason for their decision gives the first of the advantages mentioned earlier. A larger reserve of breathing medium, compared to cylinders of the same capacity tapped to the standard 200 bar, is a solid argument. But is this reserve really that much larger? To find out, it is necessary to take a closer look at the properties of the gas that is being compressed. Let’s take air as the object of our deliberations, since it is currently the most popular breathing mixture used in diving (and this is unlikely to change).
What exactly is gas?
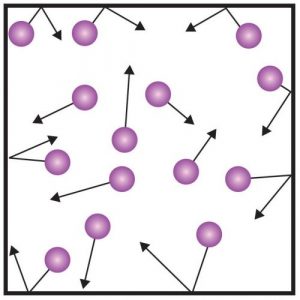
A gas is, of course, a state of matter in which the particles move freely in any direction. There are no strong interactions or relations between these molecules except that they collide with each other. In addition, if the gas is enclosed in a sealed vessel, the particles also hit the walls of the vessel. These impacts exert a certain pressure on walls of the vessel, which we can read from the pressure gauge. The figure to the right shows a diagram illustrating the behavior of gas molecules in a sealed vessel.
Ideal gas and Clapeyron’s equation.
However, the description above applies to the so-called ideal gas. This is a kind of simplified model that allows to describe many phenomena involving the gaseous state of matter with a good approximation. Such models are widely used in physics and chemistry to more clearly describe all sorts of principles and processes using textual description or mathematical formulas. We can describe gas as a state of aggregation by four main parameters: the number of gas molecules (given in units called moles), the volume occupied by gas quantity, temperature and pressure. All of these measures are dependent on each other, and their interrelationship is described by Clapeyron’s equation shown below.
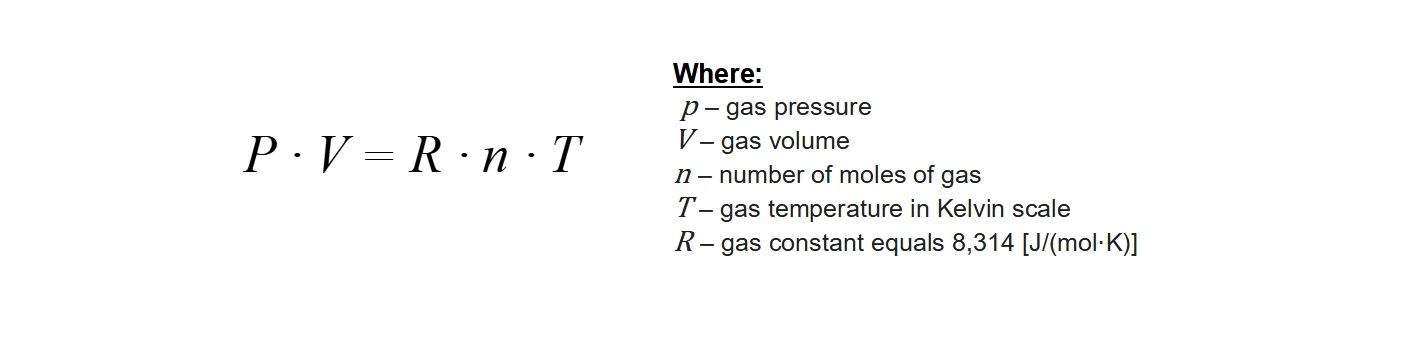
This equation is the basis of many fundamental laws used in diving, including the Boyle’s law learned on the Open Water Diver course. By appropriately transforming Clapeyron’s equation, we can calculate how much gas is in our diving cylinder. We simply have to check readings of our pressure gauge and know the volume of the cylinder with which we will dive. By multiplying both values, we can easily calculate the supply of our breathing gas for the dive. This is a very useful skill, because by knowing our own surface air consumption (SAC) we can calculate how much time we will be able to spend underwater at a given depth. Such calculations are learned by every diver already in the basic course so we will not elaborate on them here.
(Im)perfect model?
It can be said that everything looks very smooth. There are model examples of a gas and formulas to describe it. We can calculate the relationships between the most important parameters of gases and take the most necessary data from these parameters. So why we have doubts? Well, the model formulas used in science, even if they perfectly match to the phenomena we observe, are only an approximation of the real world around us. This can be compared to a pair of lovers which, in a romantic novel, are described as two people who love each other… However, in reality their relationship is accompanied by many other additional feelings and events. The same refers to the idea of a perfect gas in comparison to a real gas.
Impact with reality…
Remember, that an ideal gas is one in which there are no interactions (attraction/repulsion) between molecules and the sizes of the molecules are infinitely small. In real life, both of these rules are broken – relationships between molecules occur, and the molecules have certain dimensions. So why, when these parameters are known, are they disregarded from the overall model? There are two main reasons. Firstly, the inter-molecular interactions and the sizes of the molecules themselves are very small values. They are so small and insignificant that in practice they are unnoticed in – here is the key part of the sentence – certain ranges of pressure and temperature, primarily those that occur naturally on Earth. The second reason is presented below. This is also an equation describing the dependence of gas parameters, but this time of a real gas.

Beautiful, isn’t it? This formula is called the van der Waals equation, and it describes exactly the same relationships as Clapeyron’s equation. The difference is that, here the already mentioned interactions between gas molecules and the sizes of these molecules are taken into consideration. This can be proven in a very simple way. If we place zero for the parameters a and b the van der Waals equation will transform into the Clapeyron equation.
What’s really going on in that cylinder?
But why are we talking about this? Well, when the cylinder is filling with a breathing gas, the pressure inside increase. This fact causes the gas molecules to be closer and closer to each other, so they begin to interact more and more strongly with and have less and less space. After all, the molecules have some dimensions and there are more and more of them! When we filling the cylinder to the standard 200 bar these interactions do not matter that much (why is not matter will be explained a little later). At 300 bar the situation is different. It will be much easier to understand this on a diagram. As an example, let’s assume that two identical 24-liter (2×12) twinsets were filled, one to a pressure of 200 bar, while the other to a pressure of 300 bar. Based on Clapeyron’s (ideal gas) and van der Waals’ (real gas) formulas, the graph below shows the relationship between the number of liters of gas (axis x) and the pressure (axis y) in the cylinder.
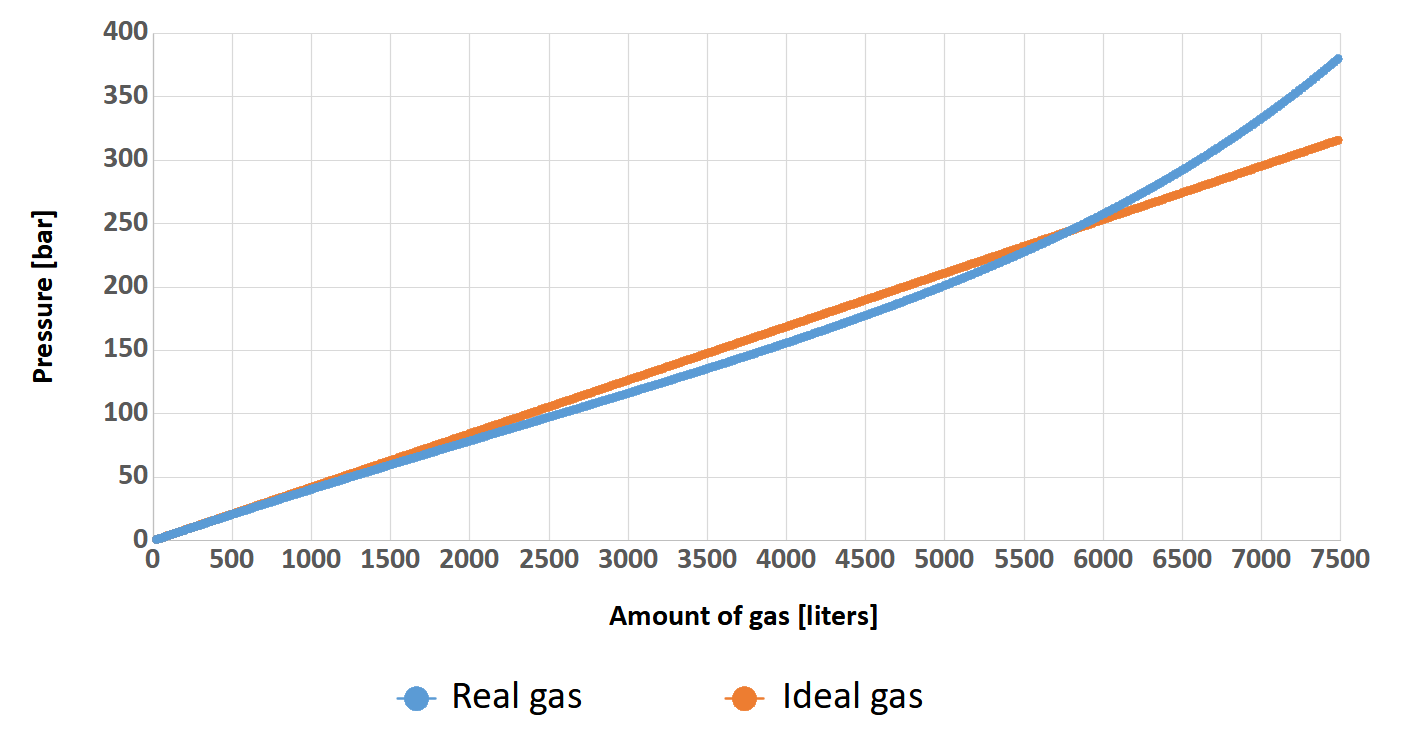
You can clearly see that at the beginning, the relationship between pressure and amount of gas in the cylinder for both gases is identical. Such state persists more or less up to a value of 100 bar (the pressure on Earth is approximately 1 bar) and can therefore be described by Clapeyron’s equation. Beyond this value, the curve of real gas no longer increases as rapidly as that of perfect gas.. This fact is mediated by inter-particle interactions that are still small at this point. In other words, the gas molecules are “stuffed” in the cylinder and there is still so much space that this comes easily. The situation change when the pressure exceeds 230 bar. We can clearly see that despite the large increase in cylinder pressure, the number of gas molecules grow slightly. At this point the inter-particle forces begin to play an important role in gas mechanics and make the Clapeyron equation begin to lose its meaning. Here is the moment where the van der Waals equation should be used.
200 bar vs 300 bar – how big is the difference?
The most interesting, is the fact that these two curves intersect around the pressure value of 220 bar. Could it be that this is what determined the choice of such a value for the working pressure of most diving cylinders? It is quite possible that it influenced this decision. Nevertheless, this is the reason that in diving we can successfully use the less complicated Clapeyron’s equation for calculations. However, let’s return to our graph. For greater readability and understanding, I will post it below once again with additional description in the form of arrows with values indicating the number of liters of gas.
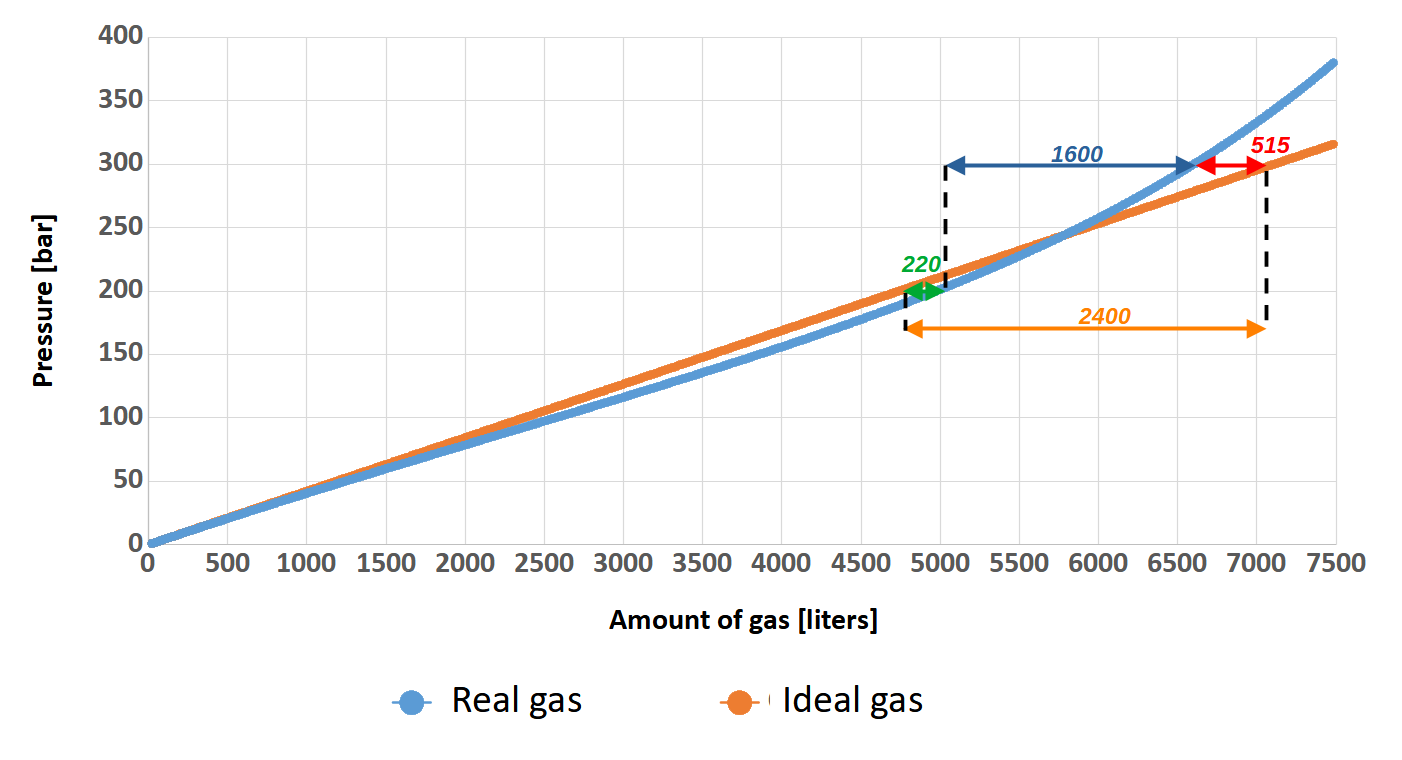
Theoretically (orange curve – author’s note), by filling our 24-liters twinset to 300 bar instead of 200 bar, we would have 2400 liters more gas in it (orange arrow). Quite a good result, right? This amount of gas allows a diver with a SAC of 20 l/min to breathe at a depth of 40 meters for 23 minutes! That’s a very large amount of time….
And what is it really like? It’s time to compare these two graphs. For a pressure value of 200 bar, which is the pressure used by most divers, the difference in the amount of gas stored between the ideal model (orange curve) and the real model (blue curve) is about 220 liters (green arrow). So we can say that we have a little more gas in the cylinder than we would expect. On the other hand, for a pressure of 300 bar comparing the ideal model and the real model (red arrow), the calculations show that we expect to have almost 515 liters more gas in reserve than there actually is. The truth is, that this 100 bar of gas will only make our supply of breathing medium increase by 1600 liters (blue arrow).
A short summary.
Thus, when considering the choice between 200-bar and 300-bar cylinder, it is worth considering all the benefits and drawbacks of such solution. Not by looking at it only through the prism of ergonomics of the set, but also the economy of breathing gas. Especially, when their actual properties at such extreme pressures differ significantly from those of the model.

About the author:
Daniel Popławski is an experienced IDF Master Diver Instructor from Masuria region. He is the author of many training presentations used by IDF instructors. With MSc in chemistry, Daniel applies his knowledge to the more scientific aspects of diving, such as gas blending. Privately, he enjoy a healthy lifestyle and all physical activity related to water (not necessarily in a liquid state). With his responsible and enthusiastic attitude he infects new diving students.




